Why Not Wolfram Alpha?

This page is outdated. When I first wrote this back in 2015, the main frustration I had was that Wolfram Alpha sometimes didn’t understand what I was asking, while Maxima can take a calculation in unambiguous mathematical notation. In the years since, Wolfram Alpha seems to have gotten better at understanding requests and it has also introduced a “math input” mode. As a result, the main disadvantage of Wolfram Alpha I point out here is no longer valid.

I still believe Maxima has other advantages over Wolfram Alpha. Maxima’s numerical analysis functionality is much more flexible than Wolfram Alpha’s. Also, Maxima runs on your own computer, so you can still use it without an Internet connection, unlike Wolfram Alpha. And Maxima is free and open-source software (FOSS), which is important to some people (myself included).

The original contents are below. I have updated the Maxima screenshots with a newer version of wxMaxima, but the Wolfram Alpha screenshots are of the original version from 2015.

---

Don’t get me wrong: Wolfram Alpha is great, and also free of charge. But it doesn’t do everything. Also, while most of the time it understands what you want, sometimes it just doesn’t.

Of course, Maxima can’t replace Wolfram Alpha for accessing real-world data, but Wolfram Alpha is often used for purely mathematical calculations and that’ll be the focus here.

It finds the derivative of a complicated single-variable function just fine. I entered d/dx[e^e^(x^2+x+1))] and got the expected result:

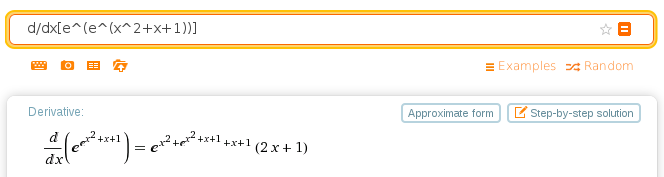
Not bad!

But when it comes to a multivariable function, things don’t go so well. I entered partial / partial x [e^e^(x^2+y+1))]:

That’s not what I meant…

Okay, I tried using plain English. I entered partial derivative with respect to x of [e^e^(x^2+y+1))], but still no luck:

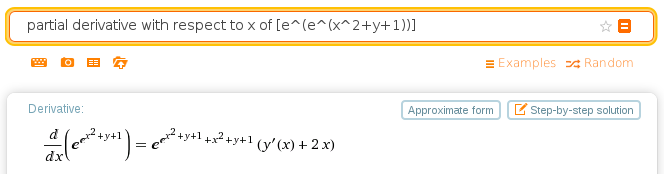
That’s close, but I mean for x and y to be independent variables.

But it works when I ask for a second-order derivative, as in second partial derivative with respect to x of [e^e^(x^2+y+1))]:

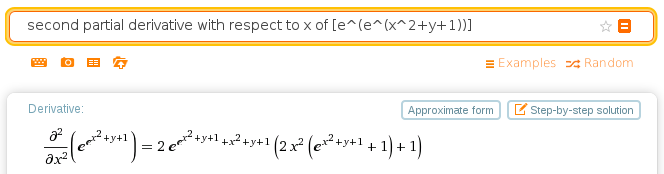
How does this work and the other not?

Maxima handles both pretty easily:

• First-order partial derivative: diff(%e^%e^(x^2+y+1), x);
• Second-order partial derivative: diff(%e^%e^(x^2+y+1), x, 2);

(The percent signs before the e’s indicate that it is the constant, not an arbitrary variable.)

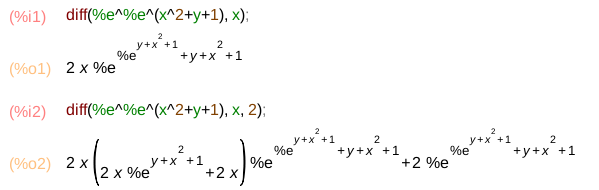
Let’s try something else. I entered jacobian r cos theta, r sin theta into Wolfram Alpha:

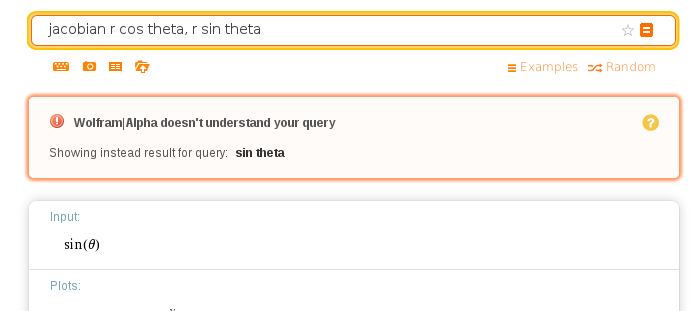
Hm…

Maybe if I’m a bit more explicit? I tried entering jacobian of (r cos theta, r sin theta). Still no:

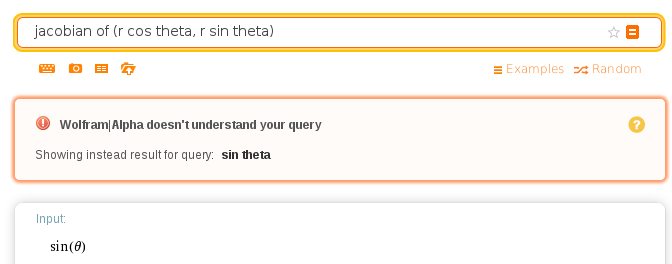
Maxima: No guessing, instant answers:

• Jacobian matrix: jacobian([r*cos(theta), r*sin(theta)]);
• Determinant: determinant(%);
• Simplify using trigonometric identities: trigsimp(%);

(The percent sign here means “previous result,” like the “Ans” key on a calculator.)